adam77 wrote:
So what does 'more certainty' mean?
Check out the probabilities of getting
'x' or more hits from 3 units for the 2 options...
Code:
2x4+ 1x2+
p(1 or more) .98 .99
p(2 or more) .89 .93
p(3 or more) .66 .58
p(4 or more) .34 -
p(5 or more) .11 -
p(6 or more) .02 -
So if the attacker's thought process is "so long as i get at least 2 hits, then it's worthwhile attacking; any extra hits over and above the first two are
insignificant", then he gains a
4% 'certainty' bump. That's not much. In return he sacrifices 12% average extra hits.
It would have to be pretty exceptional circumstances for me to choose 1x2+ over 2x4+.
(cue someone pointing out a mistake in my reasoning and making me look stupid) 
Your stats are fine and that is indeed true, but the "parity point" does depend how many units you have and I think your number of units is fairly low as an example. If you increase the number of units to 5, it is now
3 hits or more. That is, both CC stats have about the same chance of getting 3 or more hits (96% for 2+ vs 95% for 2x4+). For a formation of 8 units this "parity point" goes up again to between 5 and 6 hits.
Basically what this means is that, even though 2x4+ has a rather substantially lower average number of hits than 1x2+, 8 units actually have the same (slightly higher in fact) probability of getting at least 5 hits. Depending on your perspective, you might say that's good enough or you might not. Given first strike, your likelihood of winning the assault with 5 hits will depend most on your target's armour value, but remember you have a 97% chance of getting this result, and still a very high chance of getting more. This makes them a very predicable/dependable unit. If you think you need more like 8 hits then you're playing a risky strategy using 2x4+ stealers in this way, with only a 50% chance of getting this. You are likely to conclude they are poor performers as a result. If you want 12 hits, this is incredibly unlikely.
Working out below:
5 dice, 2+
chance of 0 = 1 * ( 1/6 * 1/6 * 1/6 * 1/6 * 1/6 ) = 1/7776
chance of 1 = 5 * ( 5/6 * 1/6 * 1/6 * 1/6 * 1/6 ) = 25/7776
chance of 2 = 10 * ( 5/6 * 5/6 * 1/6 * 1/6 * 1/6 ) = 250/7776
chance of 3 = 10 * ( 5/6 * 5/6 * 5/6 * 1/6 * 1/6 ) = 1250/7776
chance of 4 = 5 * ( 5/6 * 5/6 * 5/6 * 5/6 * 1/6 ) = 3125/7776
chance of 5 = 1 * ( 5/6 * 5/6 * 5/6 * 5/6 * 5/6 ) = 3125/7776
chance of 2 or more = 7750/7776 = 1
chance of 3 or more = 7500/7776 = 0.96
chance of 4 or more = 6250/7776 = 0.80
chance of 5 = 3125/7776 = 0.40
10 dice, 4+
chance of 0 = 1/2 ^ 10 = 1/1024
chance of 1 = 10 * 1/2 ^ 10 = 10/1024
chance of 2 = 45/1024
chance of 3 = 120/1024
chance of 4 = 210/1024
chance of 5 = 252/1024
chance of 6 = 210/1024
chance of 2 or more = 1013/1024 = 0.99
chance of 3 or more = 1 - (45+10+1/1024) = 0.95
chance of 4 or more = 1 - (120+45+10+1)/1024 = 0.83
chance of 5 or more = 1 - (210+120+45+10+1)/1024 = 638/1024 = 0.62
8 dice, 2+
chance of 0 = 1/6 ^ 8 = 1/1,679,616
chance of 1 = 8 * 1/6 ^ 7 * 5/6 = 40/1,679,616
chance of 2 = 28 * 1/6 ^ 6 * 5/6 ^ 2 = 700/1,679,616
chance of 3 = 56 * 1/6 ^ 5 * 5/6 ^ 3 = 7000/1,679,616
chance of 4 = 70 * 1/6 ^ 4 * 5/6 ^ 4 = 43,750/1,679,616
chance of 5 = 56 * 1/6 ^ 3 * 5/6 ^ 5 = 175,000/1,679,616
chance of 3+ = 1,678,875/1,679,616 = 1
chance of 4+ = 1,671,875/1,679,616 = 1
chance of 5+ = 1,628,125/1,679,616 = 0.97
chance of 6+ = 1,453,125/1,679,616 = 0.87
16 dice, 4+
chance of 0 = 1/65,536
chance of 1 = 16/65,536
chance of 2 = 120/65,536
chance of 3 = 560/65,536
chance of 4 = 1820/65,536
chance of 5 = 4368/65,536
chance of 3+ = 65,399/65,536 = 1
chance of 4+ = 64,839/65,536 = 0.99
chance of 5+ = 63,019/65,536 = 0.96
chance of 6+ = 58,651/65,536 = 0.89






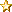

 , i.e. 1x2+ and 2x4+ are more or less equivalent for lower numbers of required hits. 2x4+ gets significantly better in situations where you need more
, i.e. 1x2+ and 2x4+ are more or less equivalent for lower numbers of required hits. 2x4+ gets significantly better in situations where you need more 